「倍率が割り切れない比例問題の解き方」の版間の差分
ナビゲーションに移動
検索に移動
編集の要約なし |
編集の要約なし |
||
| 1行目: | 1行目: | ||
{{Point|3→1などの倍率は割り切れないため、「(1÷3)倍」のまま比例を考える。}} | {{Point|3→1などの倍率は割り切れないため、「(1÷3)倍」のまま比例を考える。}} | ||
[[メディア:YenFor1ItemWhen300YenIn3itemsTwoUpwardArrowsWithOneRateInstruction.mp4|動画と音声での説明]] | [[メディア:YenFor1ItemWhen300YenIn3itemsTwoUpwardArrowsWithOneRateInstruction.mp4|動画と音声での説明]] | ||
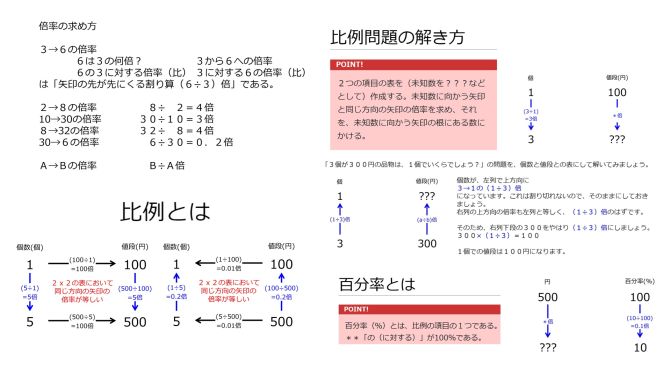
[[ファイル: | [[ファイル:ProportionInstructionSummary-Basic-Jpn.jpg|671px|none]] | ||
{{QuizTitle}} | {{QuizTitle}} | ||
<GIFT> | <GIFT> | ||
2024年12月4日 (水) 12:35時点における版
POINT!
| 3→1などの倍率は割り切れないため、「(1÷3)倍」のまま比例を考える。 |
Challenge Quiz
1.
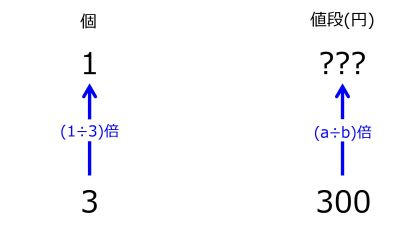
3個の値段が300円の品は、1個の値段はいくら?を解くために表を作った。
aに入る数値は
である。
bに入る数値は
である。
1個の値段は
円である。

2.

3個の値段が300円の品は、1個の値段はいくら?を解くために表を作った。
aに入る数値は
である。
bに入る数値は
である。
1個の値段は
円である。

3.
3個の値段が300円の品は、1個の値段は
円である。