「比例とは-1」の版間の差分
編集の要約なし |
編集の要約なし |
||
| 23行目: | 23行目: | ||
//LEVEL:2 | //LEVEL:2 | ||
[[画像:YenFor3When100YenFor1quiz01.jpg|250px|right]] | [[画像:YenFor3When100YenFor1quiz01.jpg|250px|right]] | ||
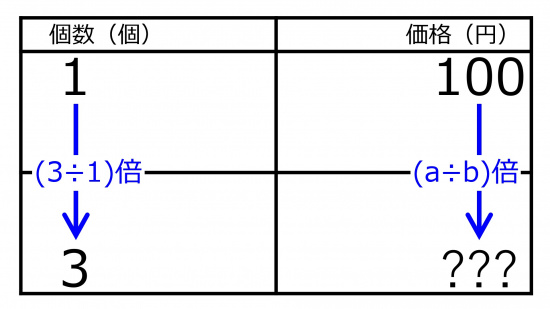
「1個が100円の品物は、3個でいくらでしょう?」の問題を、個数と価格との表を作った。aに入る数値は<br style="clear:both;" />(100の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (10の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (1の位){~0~1~2~=3~4~5~6~7~8~9}である。<br style="clear:both;" />bに入る数値は<br style="clear:both;" />(100の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (10の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (1の位){~0~=1~2~3~4~5~6~7~8~9}である。<br style="clear:both;" /><br style="clear:both;" /> | 「1個が100円の品物は、3個でいくらでしょう?」の問題を、個数と価格との表を作った。aに入る数値は<br style="clear:both;" />(100の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (10の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (1の位){~0~1~2~=3~4~5~6~7~8~9}である。<br style="clear:both;" />bに入る数値は<br style="clear:both;" />(100の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (10の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (1の位){~0~=1~2~3~4~5~6~7~8~9}である。<br style="clear:both;" /><br style="clear:both;" />3個の価格は<br style="clear:both;" />(100の位){~0~1~2~=3~4~5~6~7~8~9}<br style="clear:both;" /> (10の位){~=0~1~2~3~4~5~6~7~8~9}<br style="clear:both;" /> (1の位){~=0~1~2~3~4~5~6~7~8~9}円である。 | ||
2022年11月1日 (火) 10:37時点における版
| 「同じ方向の矢印の倍率が等しい」2つの項目の関係。たとえば、「100均ストア」において、個数が1個→5個と5倍になると、価格も100円→500円と5倍になる関係。 |
「100均ストア」でのお買い物での個数と価格との間に比例関係があります。個数と価格で表を作って考えてみましょう。個数が、左列で下方向に
1個→5個の(5÷1=)5倍
になると、価格も、右列で下方向に
100円→500円の(500÷100=)5倍
になっています。
「同じ方向の矢印の倍率が等しい」
が比例の表の特徴です。
「1個が100円の品物は、3個でいくらでしょう?」の問題を、個数と価格との表にして解いてみましょう。個数が、左列で下方向に
1→3の(3÷1=)3倍
になっています。右列の下方向の倍率も等しいはずです。
そのため、右列の100円をやはり3÷1=3倍にしましょう。
100×3÷1=300
3個での価格は300円になります。
Challenge Quiz
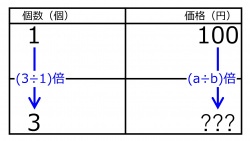
「1個が100円の品物は、3個でいくらでしょう?」の問題を、個数と価格との表を作った。aに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
bに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
3個の価格は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 円である。
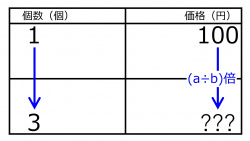
「1個が100円の品物は、3個でいくらでしょう?」の問題を、個数と価格との表を作った。aに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
bに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
3個の価格は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 円である。
1個の価格が100円の品物の、3個の価格は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 円である。
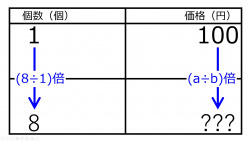
「1個が100円の品物は、8個でいくらでしょう?」の問題を、個数と価格との表を作った。aに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
bに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
8個の価格は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 円である。
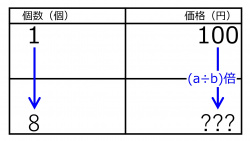
「1個が100円の品物は、8個でいくらでしょう?」の問題を、個数と価格との表を作った。aに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
bに入る数値は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 である。
1個の価格は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 円である。
1個の価格が100円の品物の、8個の価格は
(100の位) 0 1 2 3 4 5 6 7 8 9
(10の位) 0 1 2 3 4 5 6 7 8 9
(1の位) 0 1 2 3 4 5 6 7 8 9 円である。