POINT!
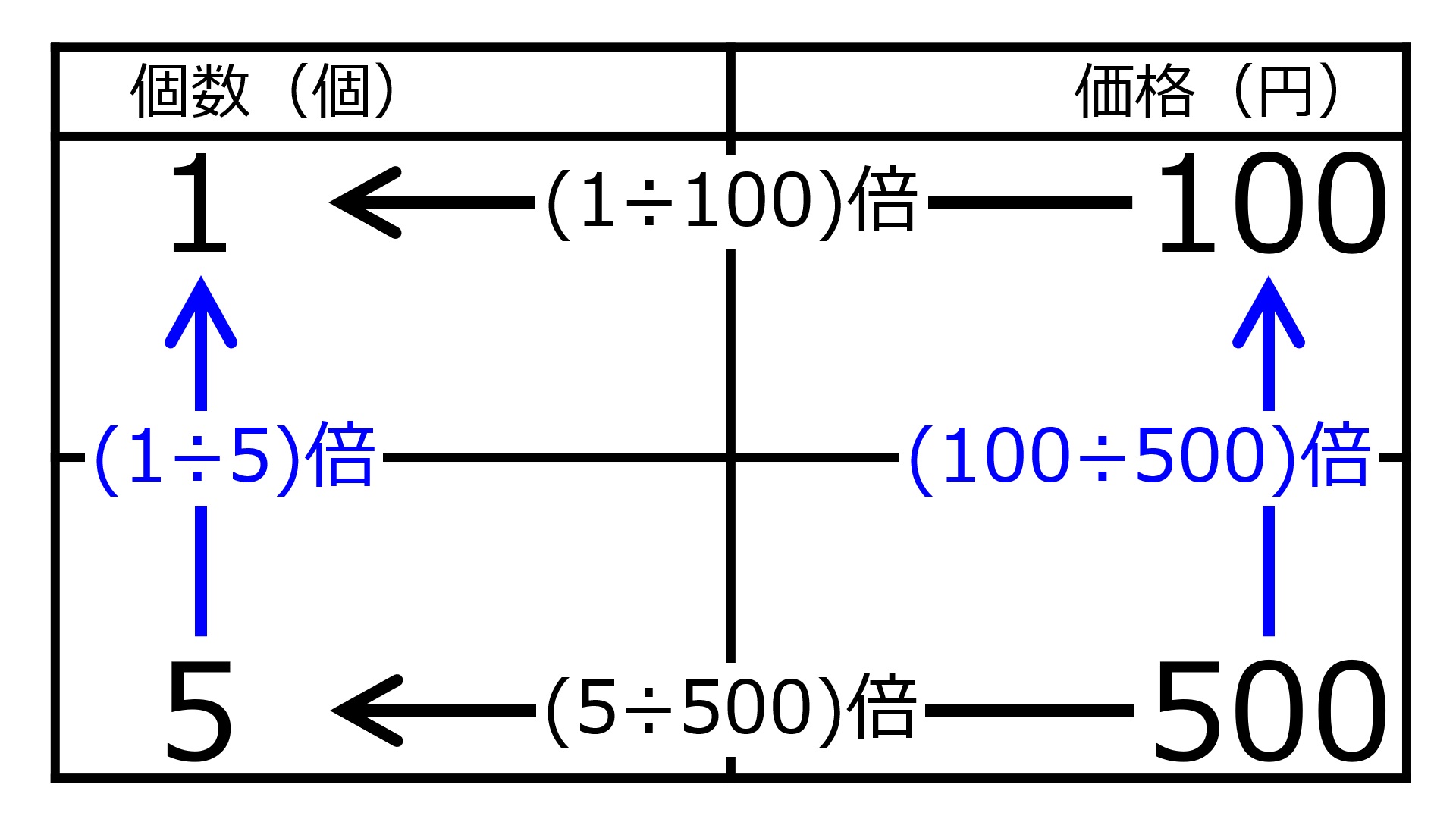
| 比例の表は縦、横、どの方向にも倍率は等しい。 |
１個１００円、５個で５００円の表を逆の方向で倍率を求めてみましょう。
左方向に、上段の
１００→１の（１÷１００＝）０．０１倍
は下段の
５００→５の（５÷５００＝）０．０１倍
と等しいです。
上方向に、左列の
５→１の（１÷５＝）０．２倍
は右列の
５００→１００の（１００÷５００＝）０．２倍
と等しいです。
「同じ方向の矢印の倍率が等しい」は、上下左右のすべての方向に成り立つのです。
２個で２００円の品物は、１００円で何個買えるでしょう？の問題を、個数と価格とを表にして解いてみましょう。右列で上方向に
２００→１００個の（１００÷２００＝）０．５倍
になっています。左列の上方向の倍率も右列と等しく、a=100, b=200のはずです。
そのため、左列下段の２をやはり１００÷２００＝０．５倍にしましょう。
２×１００÷２００＝１
１００円で買える個数は１個になります。
また、下段で左方向に
２００→２個の（２÷２００＝）０．０１倍
になっています。上段の左方向の倍率も下段と等しく、c=2, d=200のはずです。
そのため、上段右列の１００をやはり２÷２００＝０．０１倍にしましょう。
１００×２÷２００＝１
１００円で買える個数は１個になります。
Challenge Quiz
1.
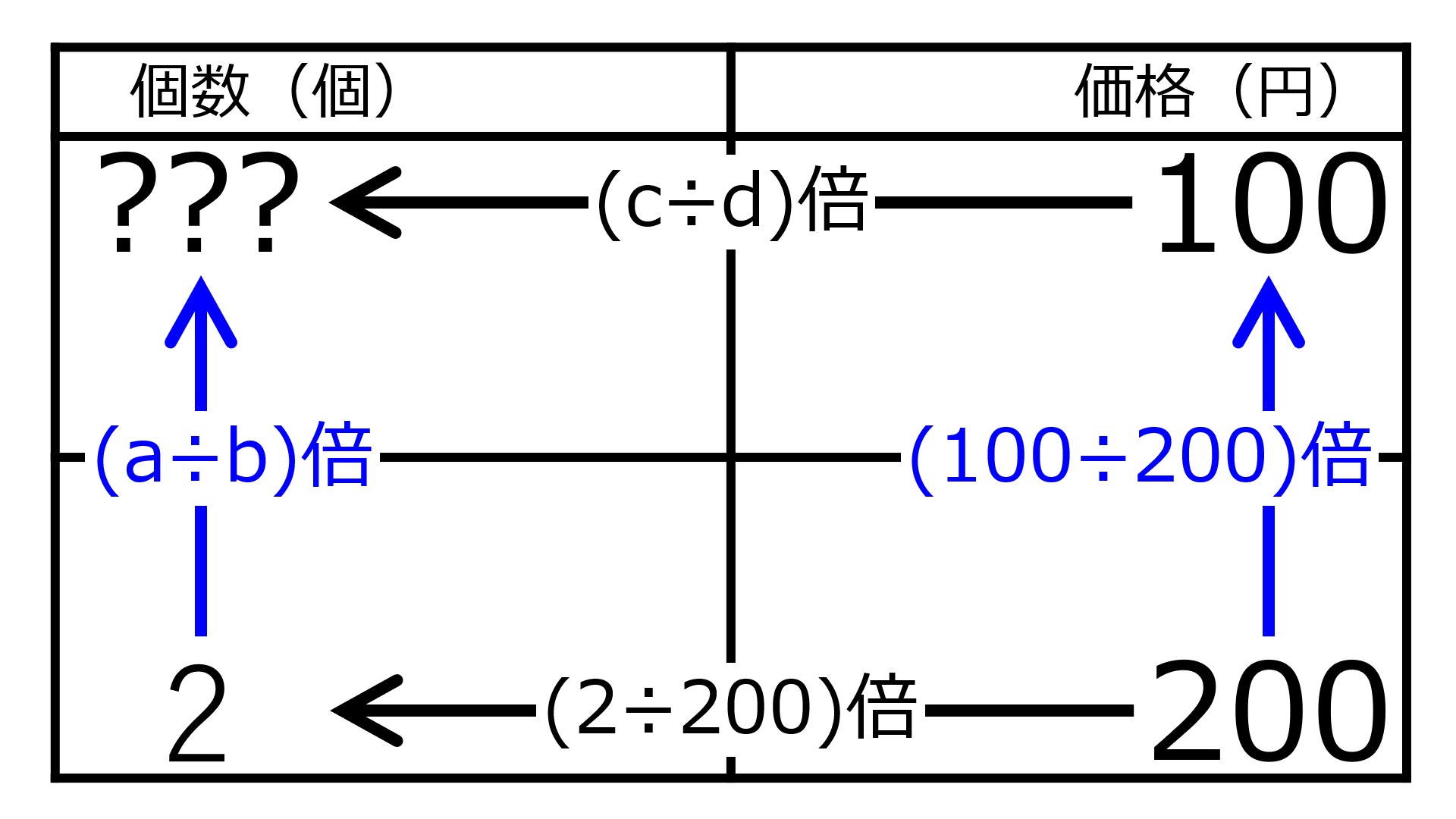「２個で２００円の品物は１００円で何個買える？」を解くために個数と価格との表を作った。ａに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｂに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｃに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｄに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
１００円で買える個数は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個である。
「２個で２００円の品物は１００円で何個買える？」を解くために個数と価格との表を作った。ａに入る数値は（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｂに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｃに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｄに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
１００円で買える個数は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個である。
2.
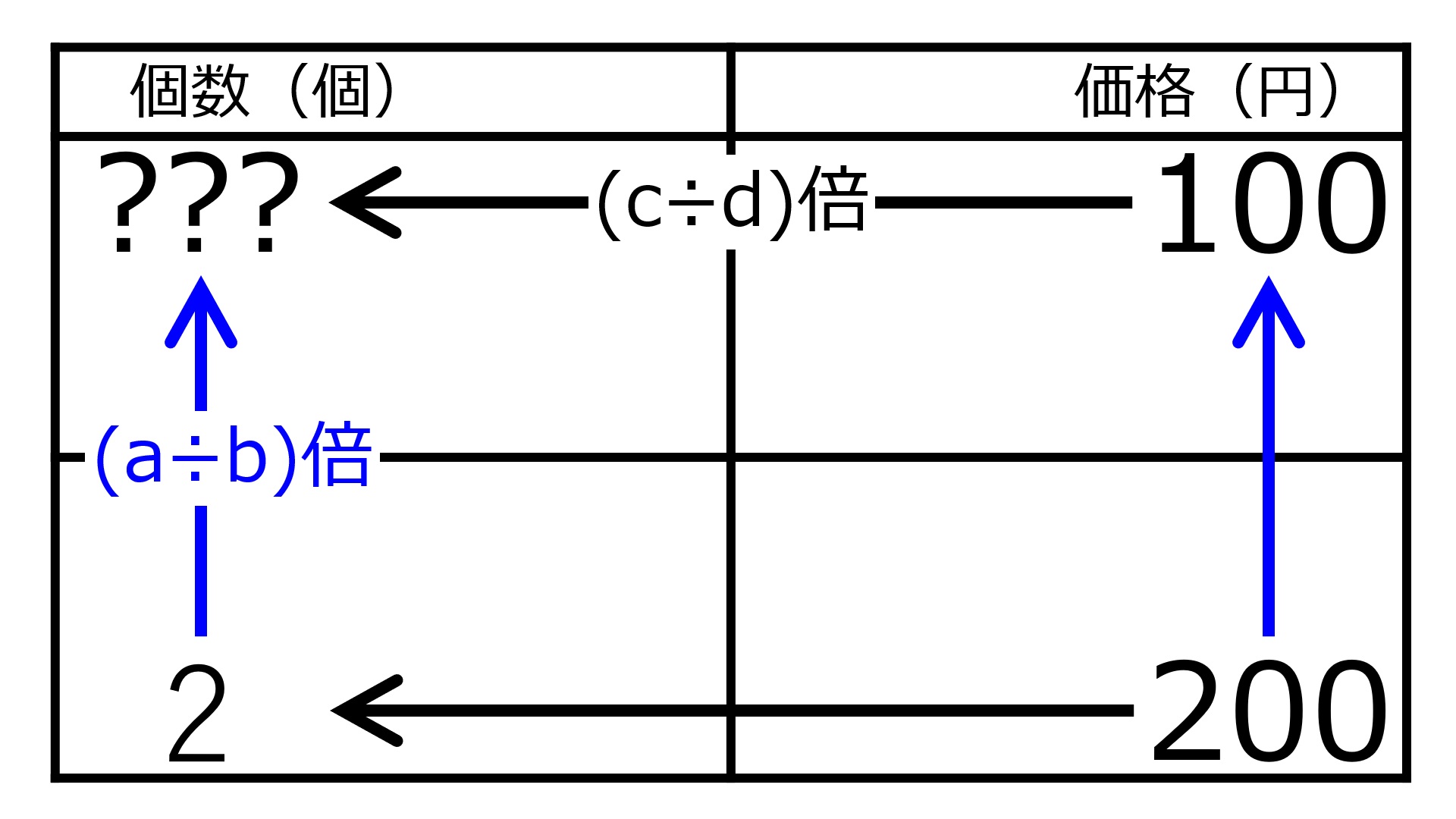「２個で２００円の品物は１００円で何個買える？」を解くために個数と価格との表を作った。ａに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｂに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｃに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｄに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
１００円で買える個数は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個である。
「２個で２００円の品物は１００円で何個買える？」を解くために個数と価格との表を作った。ａに入る数値は（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｂに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｃに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
ｄに入る数値は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 である。
１００円で買える個数は
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個である。
3.
２個で２００円の品物は１００円で
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
4.
４個で８００円の品物は２００円で
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
5.
２個で４００円の品物は６００円で
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
6.
２個で５０円の品物は７５円で
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
7.
４個で６０円の品物は１５０円で
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。
（１００の位） 0 1 2 3 4 5 6 7 8 9
（１０の位） 0 1 2 3 4 5 6 7 8 9
（１の位） 0 1 2 3 4 5 6 7 8 9 個買える。